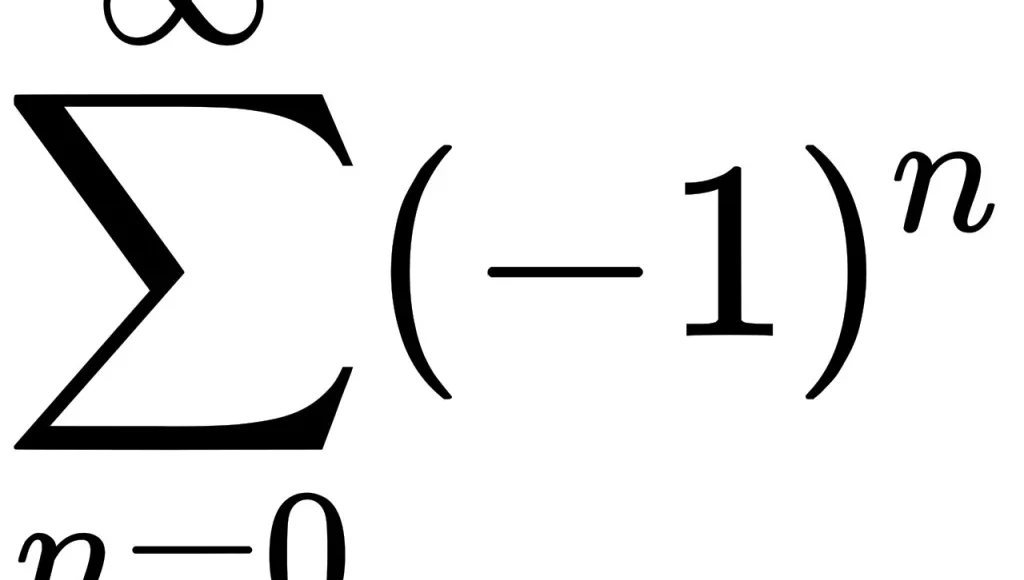Ποιά είναι τιμή του αθροίσματος 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + …
Α) 0
Β) 1
Γ) ½
Δ) δεν ορίζεται
Η ερώτηση αν και φαίνεται πολύ απλή, προβλημάτισε μερικούς από τους μεγαλύτερους μαθηματικούς του 18ου αιώνα. Την περιβάλλει μια παραδοξότητα, αφού επιδέχεται εντελώς διαφορετικές απαντήσεις βασισμένες όλες σε λογικά επιχειρήματα.
Το 1703, ο Ιταλός μοναχός και μαθηματικός Luigi Guido Grandi ερεύνησε για πρώτη φορά το παραπάνω άθροισμα με άπειρους όρους. Ο Grandi, το όνομα του οποίου φέρει το εν λόγω άθροισμα, παρατήρησε αρχικά, ότι αν το διατάξουμε ως
(1 – 1) + (1 – 1) + (1 – 1) + … = 0 + 0 + 0 + …
τότε το άθροισμα ισούται με 0.
Όμως, με μια μικρή μετατόπιση των παρενθέσεων
1 + (–1 + 1) + (–1 + 1) + (–1 + 1) + … = 1 + 0 + 0 + 0 + …
παίρνουμε μια εντελώς διαφορετική τιμή – το άθροισμα τώρα ισούται με 1.
Οι δυο συλλογιστικές παρότι δίνουν τα αντικρουόμενα αποτελέσματα 0 και 1, φαίνονται εξίσου λογικοφανείς. Αλλά και η τρίτη επιλογή, το ½, έχει κι αυτή τη «λογική» της. Πώς όμως είναι δυνατόν ένα άθροισμα άπειρων ακεραίων να δώσει ως αποτέλεσμα ένα κλάσμα; Ο Grandi και πολλοί εξέχοντες μαθηματικοί του 18ου αιώνα μετά από αυτόν, κατέληξαν ότι η απάντηση θα μπορούσε να είναι όντως ½. Ο Grandi δικαιολόγησε αυτό το αποτέλεσμα με μια παραβολή: φανταστείτε ότι δύο αδέρφια κληρονομούν έναν μόνο πολύτιμο λίθο από τον πατέρα τους και ο καθένας τον φυλάσσει διαδοχικά στο δικό του σπίτι για έναν χρόνο, εναλλάξ. Αν συνεχιζόταν αυτή η παράδοση της παράδοσης του πολύτιμου λίθου πέρα δώθε με τους απογόνους τους, τότε οι δύο οικογένειες θα είχαν η καθεμία την μισή ιδιοκτησία πάνω στο πετράδι.
Αλλά και χωρίς παραβολές, θέτοντας S = 1 − 1 + 1 − 1 + …, τότε 1 − S = 1 − (1 − 1 + 1 − 1 + …) = 1 − 1 + 1 − 1 + … = S, οπότε 1 − S = S ή S = ½ = 1 − 1 + 1 − 1 + …
Αυτή η αριθμητική ασυνέπεια, ότι 1 − 1 + 1 − 1 + … = (1 – 1) + (1 – 1) + (1 – 1) + … = 0 = 1 + (–1 + 1) + (–1 + 1) + (–1 + 1) + … = 1 ή 1/2 είχε θεολογική σημασία για τον Grandi, ο οποίος πίστευε ότι απέδειξε πως η δημιουργία από το τίποτα ήταν «απόλυτα εύλογη». Κι αυτό εξηγούσε ότι ο Θεός δημιούργησε κάτι (τον κόσμο) από το μηδέν.
Ο διάσημος μαθηματικός Gottfried Wilhelm Leibniz συμφωνούσε με την επιλογή ½, και προσπάθησε να την υποστηρίξει πιο άμεσα με πιθανολογικό συλλογισμό. Ο Leibniz υποστήριξε ότι αν σταματήσετε να αθροίζετε τις σειρές σε ένα τυχαίο σημείο, τότε το άθροισμά σας μέχρι αυτό το σημείο θα είναι είτε 0 είτε 1 με ίση πιθανότητα, επομένως είναι λογικό να επιλέξετε ως αποτέλεσμα τον μέσο όρο τους το ½. Ο Leibniz θεώρησε ότι το αποτέλεσμα ήταν σωστό, αλλά αναγνώρισε ότι το επιχείρημά του ήταν περισσότερο «μεταφυσικό παρά μαθηματικό». Ο Leonhard Euler χρησιμοποίησε πιο περίπλοκες μεθόδους για να υποστηρίξει το ½ και στην εργασία του On Divergent Series του 1760, γράφει: «δεν υπάρχει αμφιβολία ότι στην πραγματικότητα η σειρά 1 – 1 + 1 – 1 + 1 – 1 + κ.λπ. και το κλάσμα 1/2 είναι ισοδύναμες ποσότητες και ότι επιτρέπεται πάντα η αντικατάσταση του ενός με το άλλο χωρίς σφάλμα.» Έτσι, πολλοί έξυπνοι άνθρωποι έκλιναν προς την επιλογή Γ, το ½.
Οι μαθηματικοί έκαναν ένα ουσιαστικό βήμα προς την επίλυση του μυστηρίου της σειράς του Grandi στα τέλη του 19ου αιώνα. Από τα θεμέλια του απειροστικού λογισμού προέκυψαν διευκρινιστικοί ορισμοί σχετικά με το πότε οι άπειρες σειρές αθροίζονται δίνοντας πεπερασμένες τιμές. Η εύρεση της απάντησης ξεκινά με την εξέταση μερικών αθροισμάτων – προσθέστε τους δύο πρώτους όρους, μετά τους τρεις πρώτους, μετά τους τέσσερις πρώτους και ούτω καθεξής. Αν αυτά τα ενδιάμεσα αθροίσματα συνεχίσουν να πλησιάζουν όλο και περισσότερο προς μια σταθερή τιμή, τότε λέμε ότι η σειρά «συγκλίνει» σ’ αυτή την τιμή.
Τα μερικά αθροίσματα της σειράς Grandi (1, 1–1=0, 1–1+1=1, 1–1+1–1=0, 1–1+1–1+1=1, …) δίνουν εναλλάξ τις τιμές 0 και 1 χωρίς να συγκλίνουν σε μία μόνο τιμή. Έτσι, οι σύγχρονοι μαθηματικοί θα προτιμούσαν την επιλογή Δ – ότι η σειρά του Grandi δεν συγκλίνει σε κάποια τιμή.
Η επίλυση της σειράς του Grandi εγείρει ένα κοινωνιολογικό ερώτημα. Γιατί η μαθηματική κοινότητα αποδέχεται την προσέγγιση των μερικών αθροισμάτων αλλά όχι το πιθανολογικό επιχείρημα του Leibniz ή κάποιον άλλο ορισμό της άθροισης μιας άπειρης σειράς; Αν και μπορεί να μοιάζουν και να έχουν παρόμοια μυρωδιά, το άθροισμα μιας άπειρης σειράς δεν είναι το ίδιο με την πρόσθεση. Για παράδειγμα είναι ξεκάθαρο ότι η πρόσθεση δεν αλλάζει όταν αλλάζουμε παρενθέσεις, π.χ. 1 + (2 + 3) = (1 + 2) + 3. Όμως πολλές απειροσειρές, συμπεριλαμβανομένης της σειράς Grandi, το κάνουν. Για ευκολία, οι μαθηματικοί δανείζονται λέξεις όπως «άθροισμα» και «ίσον» από την πρόσθεση για να συζητήσουν περί σειρών, αλλά στην ουσία αυτό που πραγματικά εννοούν όταν λένε ότι η τάδε σειρά «έχει άθροισμα S» ή «ισούται με S», είναι ότι τα μερικά αθροίσματα συγκλίνουν στην τιμή S – τίποτε περισσότερο και τίποτε λιγότερο.
Ο ορισμός της σύγκλισης με τα μερικά αθροίσματα είναι ένας ορισμός που επιλέγεται από τους ανθρώπους. Αυτό δεν τον κάνει αυθαίρετο. Η κοινότητα των μαθηματικών προτιμά τον ορισμό από τις εναλλακτικές απόψεις για πολλούς και ορθούς λόγους. Μετριάζει πολλά από τα παράδοξα που ταλάνιζαν παλαιότερους μαθηματικούς όταν μελετούσαν άπειρα αθροίσματα, και διατηρεί πολλές από τις ωραίες ιδιότητες που απολαμβάνει η πεπερασμένη πρόσθεση. Αλλά υπάρχουν κι άλλοι ορισμοί σύγκλισης που μπορούν να εφαρμοστούν. Για παράδειγμα, αντί να ψάχνουμε ποιον αριθμό προσεγγίζουν τα επιμέρους αθροίσματα η μέθοδος άθροισης Cesàro παίρνει τον μέσο όρο των δύο πρώτων μερικών αθροισμάτων, μετά τον μέσο όρο των τριών πρώτων μερικών αθροισμάτων και μετά τα πρώτα τέσσερα μερικά αθροίσματα και ούτω καθεξής επ’ άπειρον, και έτσι αναζητούμε ποιόν αριθμό προσεγγίζουν αυτοί οι μέσοι όροι. Αν εφαρμόσουμε αυτήν την μικρο-τροποποιημένη μέθοδο σε συγκλίνουσες σειρές θα παίρνουμε πάντα το ίδιο αποτέλεσμα που δίνει και η κλασική μέθοδος. Ωστόσο, μερικές φορές παίρνουμε διαφορετικά αποτελέσματα όταν την εφαρμόζουμε σε σειρές που δεν συγκλίνουν σύμφωνα με τον καθιερωμένο ορισμό. Συγκεκριμένα, όπως είδαμε παραπάνω τα μερικά αθροίσματα της σειράς του Grandi είναι: 1, 0, 1, 0, 1, 0, 1, … και εφαρμόζοντας σε αυτά την μέθοδο του Cesàro παίρνουμε την ακολουθία των αριθμών: 1, 1/2,1/3, 2/4, 2/5, 3/6, 4/7, … η οποία τείνει στο ½.
Στην μαθηματική βιβλιογραφία εμφανίζονται κι άλλες μέθοδοι άθροισης απειροσειρών. Ακόμα κι αν μερικές φορές δίνουν διαφορετικά αποτελέσματα για την ίδια σειρά, αυτό δεν αποτελεί αντίφαση εφόσον κοινοποιείται ξεκάθαρα ο ορισμός που χρησιμοποιήθηκε. Στην πραγματικότητα, δεν μπορούμε να προσθέσουμε φυσικά έναν άπειρο αριθμό πραγμάτων, επομένως οι μέθοδοι άθροισης παρέχουν απλώς βασικούς τρόπους αντιστοίχισης τιμών σε άπειρες σειρές. Ο ορισμός των μερικών αθροισμάτων έχει το κύρος της προεπιλογής, αλλά σε κάποιες περιπτώσεις βοηθάει το να υπάρχουν κι άλλες επιλογές όταν αντιμετωπίζουμε σειρές που δεν συγκλίνουν σύμφωνα με τον ορισμό των μερικών αθροισμάτων.
Περιέργως, η σειρά του Grandi τείνει στην τιμή ½ στις περισσότερες εναλλακτικές μεθόδους. Έτσι, μια απάντηση χωρίς μαθηματική αυστηρότητα στην αρχική μας ερώτηση θα μπορούσε να είναι η εξής: η τιμή του αθροίσματος «1 – 1 + 1 – 1 + 1 – 1 + …» δεν ορίζεται, αλλά αν οριζόταν θα ήταν το 1/2.
Πηγή: physicsgg